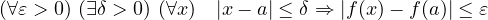
Without these tiny quantities, the technicality of analysis is very high. When one sees
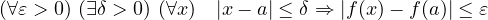
it will not appear clear to a student that we are talking about continuity.
At a time when no infinitesimals of any kind were formalised, the invention of the epsilon-delta process was a prodigious achievement but, since then, there have been improvements.
And almost everybody has some intuition about ”infinitesimal quantities” so a mathematical system in which these are shown not to exist could be simply considered too short.
For the instructor, changing will require an effort in acquiring extra knowledge which may, at times, challenge received ideas. But when one realises that continuity becomes defined by
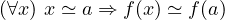
it could seem worth taking a look.